Momentum Contrast (MoCo)
In Contrastive Learning, from the representation of an augmented view of an image, our network learns to discriminate between the representation of another augmented view of the same image, and the representation of augmented view of a different image. This learning requires comparison between the representation of an augmented view and many negative samples.
For this, Momentum Contrast (MoCo) borrowed the idea of tokenized dictionaries from BERT (He et al., 2020). In MoCo, we have the query representation $q$, expressed as $q = f_q(x^q)$ where $f_q$ is encoder network and $x^q$ is an encoder query sample. Similarly, on the other side, we have a set of encoded samples ${k_0, k_1, k_2, … }$ expressed as $k = f_k(x^k)$ where $f_k$ is key encoder and $x^k$ is a sample to be compared against.
As we are comparing representation of another augmentation of same image with representation of augmentations of different image, let’s assume we have only single key $k_{+}$ in dictionary matching $q$ query, and rest are negative matches. Then, our network needs to classify $q$ as $k_{+}$. For this, MoCo uses contrastive loss called InfoNCE, where value of loss function is low when $q$ is compared to its similar key $k_{+}$ and large when compared to other dissimilar keys. Contrastive loss, InfoNCE is given below:
\[L_q = -\text{log}\frac{\text{exp}(q⋅ k_{+} / \tau)}{\sum_{i=0}^k \text{exp}(q ⋅ k_{i} / \tau)}\]where $\tau$ is a temperature hyper-parameter. In MoCo, we try to maintain a dynamic but large dictionary as a queue of data samples. This is done by decoupling queue from mini-batch, making dictionary grow larger than mini-batch size. From this queue the oldest encoded representation can be dequeued with new representation from current mini-batches (size of which can be set by parameter). This property makes it dynamic. Overview of MoCo network is given below:
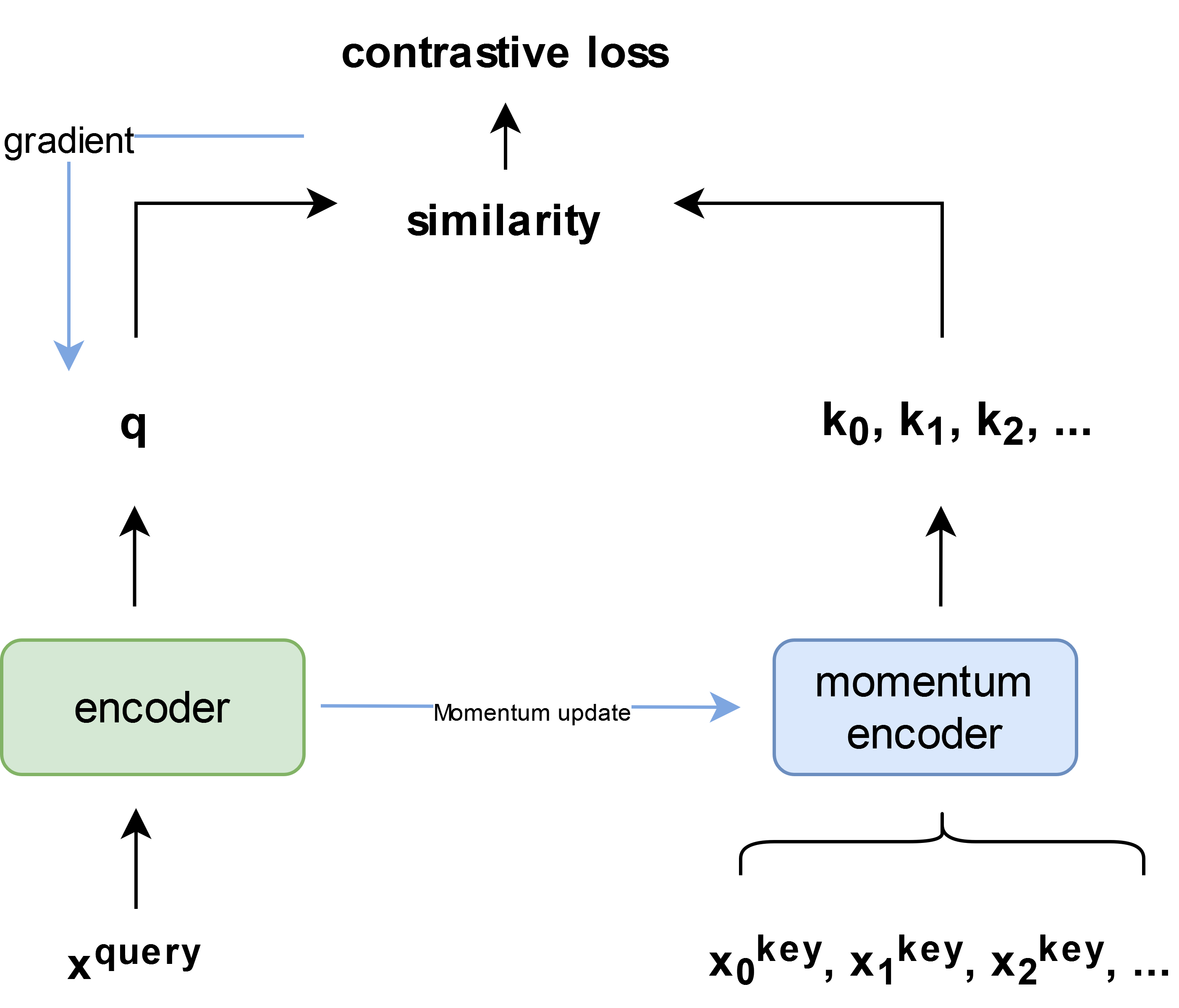
However, a faster displacement of older representations from queue can make it harder for network to minimizse loss. For this reason, a slow-moving momentum update is proposed as:
\[\theta_k ← m⋅ \theta_k + (1 - m)⋅ \theta_q\]Here, $\theta_k$ is parameter of key encoder $f_k$, and $\theta_q$ is parameter of queue of encoder. This makes $\theta_k$ evolves slowly as back-propogation from contrastive loss is not directly being added to it, but only updates the parameter $\theta_q$. Also, \(m ∈ [0,1)\) where m = 0.99 works better than m = 0.9.
BYOL
Unlike MoCo, Bootstrap Your Own Latent (BYOL) method does not uses negative pairs, and yet appears to be more effective than other contrastive methods.
In BYOL, we have two networks: online and target. Both are given different augmentation of a same image, and then we train the predictor of online network to predict representation of target. Loss calculated after prediction is back-propagated to the online network, and target network is updated with exponential moving average of online networks’ parameter (Grill et al., 2020). Overall architecture is given below:
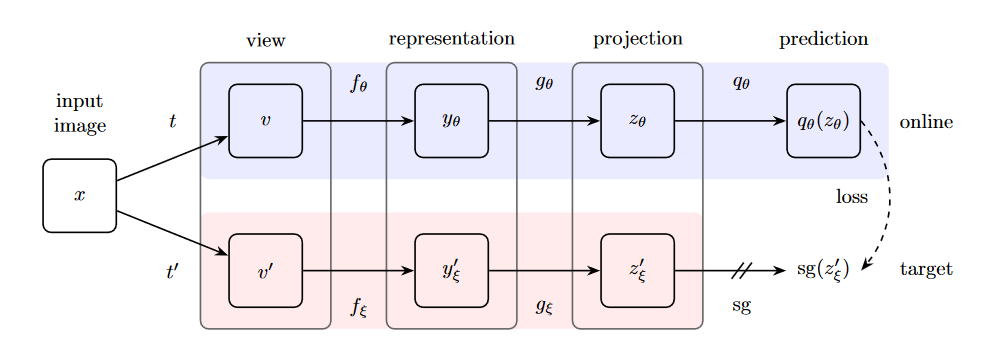
Given an input image $x$ from a set of images $D$ and two distribution of image augmentation $T$ and $\hat{T}$. BYOL, firstly, applies two augmentation $t ∼ T$ and $t’ ∼ T’$ to create two augmented views i.e., $v ≜ t(x)$ and $v’ ≜ t’(x)$.
Next, BYOL uses two networks: online and target.
Online network is defined by a set of weights $\theta$ and consists of three stages 1. encoder (generally, ResNet) $f_{\theta}$ that extracts representation from the first augmented view $v$ as $y_{\theta} ≜ f_{\theta}(v)$, 2.projector $g_{\theta}$ creating a projection $z_{\theta} ≜ g_{\theta}(y)$ and 3. predictor $q_{\theta}$.
Target network similar using another augmentation $v’$, but using different set of weights $\xi$ first extract representation from 1. encoder $f_{\xi}$ as \({y'_{\xi}} \triangleq f_{\xi}(v')\), and then provides a target projection from 2. projector $g_{\xi}$ as \({z'_{\xi}} \triangleq g_{\xi}(y')\).
Next, from the predictor of online network, we make a prediction of target projection \({z'_{\xi}}\) as \(q_{\theta}(z_{\theta})\).
Afterwards, we take L2-Normalization of both target projection and prediction to make it scale-invariant as \(\tilde{z'_{\xi}} ≜ \frac{z'_{\xi}}{\lVert z'_{\xi} \rVert^2}\) and \(\tilde{q_{\theta}(z_{\theta})} ≜ \frac{q_{\theta}(z_{\theta})}{\lVert q_{\theta}(z_{\theta}) \rVert^2}\), respectively.
In BYOL, as we intend to match online network prediction with target projection, we next try to minimise the difference between them with Mean Squared Error as:
\[L_{\theta, \xi} = \lVert \tilde{q_{\theta}(z_{\theta})} - \tilde{z'_{\xi}}\rVert^2_2\]This loss is then backpropagated to update only online weight $(\theta)$, whereas target network is not trained via gradients, target network weights $(\xi)$ are updated to be an exponential moving average of online network weight $\theta$ with a decay rate $τ ∈ [0,1]$ as:
\[ξ ← τ ⋅ ξ + (1 - τ )θ\]Next, to ensure that the model learn robust representation, and loss is symmetrized, we swap the views of image to alternate network i.e., sending $v’$ to online network, and $v$ to target network. This, eventually, gives us an alternate loss $\tilde{L_{\theta, \xi}}$ making total loss of our BYOL method as:
\[L_{\text{BYOL}} = L_{\theta, \xi} + \tilde{L_{\theta, \xi}}\]At each training step, we try to minimise this $L_{\text{BYOL}}$ with respect to $\theta$ and update $\xi$. BYOL training step can be summarized as:
\[θ ← \text{optimizer}(\theta, ∇_{θ}L_{\theta, \xi}^{\text{BYOL}}, η) \qquad \text{and}\qquad ξ ← τ ⋅ ξ + (1 - τ )θ\]SwAV
(Caron et al., 2020)
SimSiam
(Chen and He, 2021)
References
-
Caron, M., Misra, I., Mairal, J., Goyal, P., Bojanowski, P. and Joulin, A., 2020. Unsupervised learning of visual features by contrasting cluster assignments. Advances in neural information processing systems, 33, pp.9912-9924.
-
Chen, X. and He, K., 2021. Exploring simple siamese representation learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 15750-15758).
-
Grill, J.B., Strub, F., Altché, F., Tallec, C., Richemond, P., Buchatskaya, E., Doersch, C., Avila Pires, B., Guo, Z., Gheshlaghi Azar, M. and Piot, B., 2020. Bootstrap your own latent-a new approach to self-supervised learning. Advances in neural information processing systems, 33, pp.21271-21284.
-
He, K., Fan, H., Wu, Y., Xie, S. and Girshick, R., 2020. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 9729-9738).